Sidik ragam atau analysis of variance (Anova) merupakan tehnik analisis untuk menguji signifikansi perbedaan beberapa kelompok dalam sebuah populasi. Dalam prosesnya Anova memilah-milah keragaman berdasarkan kriteria tertentu. Sumber keragaman inilah yang akan dijadikan sebagai pembanding untuk mengetahui sumber mana yang menyebabkan terjadinya keragaman tersebut (Sugiarto, 2006 p. 185) Jika hanya membandingkan dua kelomppok dalam populasi yang sama maupun yang berbeda cukup dengan uji-t misalnya.
Perumusan hipotesis
| H0 | : | Tidak terdapat perbedaan antar kelompok |
| H1 | : | Setidaknya ada satu kelompok berbeda dari lainnya |
Beberapa kasus penelitian yang membutuhkan uji Anova misalnya menguji terdapat perbedaan berat badan burung bangau dalam satu baris yang terbang berkelompok. Taruhlah terdapat 4 baris yang terbang berkelompok, maka jika ada satu burung bangau saja yang beratnya berbeda signifikan dapat disimpulkan hipotesis H1 diterima.
Contoh lainnya, menguji pengaruh iklim makro ( event study ) terhadap sentimen pasar. Misalnya dilakukan pengamatan 7 hari sebelum dan sesudah periode peristiwa. Jika hanya terdapat satu hari saja indikator pasar modal (seperti abnormal return ) menunjukkan perbedaan dapat disimpulkan hipotesis H1 diterima
Contoh lainnya, menguji pengaruh iklim makro ( event study ) terhadap sentimen pasar. Misalnya dilakukan pengamatan 7 hari sebelum dan sesudah periode peristiwa. Jika hanya terdapat satu hari saja indikator pasar modal (seperti abnormal return ) menunjukkan perbedaan dapat disimpulkan hipotesis H1 diterima
Kriteria penerimaan hipotesis
- Hipotesis H0 diterima jika Fhitung ≤ Ftabel atau p ≥ 0.05
- Hipotesis H1 diterima jika Fhitung > Ftabel atau p < 0.05
Anova hanya mampu mendeteksi ada kelompok dalam satu populasi yang menyebabkan berbeda, tapi tidak mampu mendeteksi kelompok penyebab berbeda signifikan. Oleh karena itu perlu dilanjutkan dengan Post Hoc seperti uji-t, DMRT, LSD, HSD.
Dalam banyak kasus, biasanya peneliti tidak menyertakan Anova karena jika ada (minimal) salah satu kelompok yang berbeda signifikan maka dipastikan dalam populasi tersebut ada perbedaan ( Lee, 2000, p. 487).
Dalam banyak kasus, biasanya peneliti tidak menyertakan Anova karena jika ada (minimal) salah satu kelompok yang berbeda signifikan maka dipastikan dalam populasi tersebut ada perbedaan ( Lee, 2000, p. 487).
Simulasi
Dilakukan pengamatan berat badan bangau yang terbang berkelompok terdiri dari 4 baris.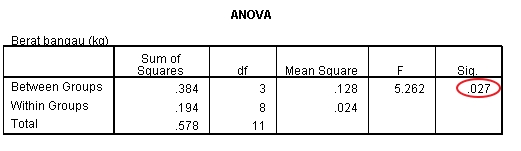
Figure 1. Output Anova
Diperoleh p (0,027) < 0.05 sehingga menolak H0 dan menerima H1. Disimpulkan minimal ada satu baris yang rata-rata berat bangaunya berbeda dengan baris yang lain. Tetapi uji F tidak menunjukkan baris bangau ke berapa yang berbeda. Oleh karena itu perlu dilakukan uji Post Hoc.
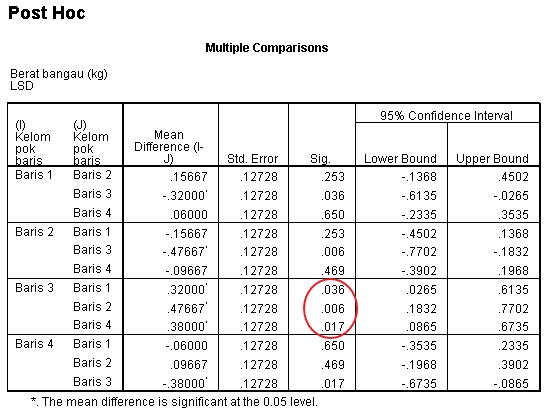Figure 2. Output Uji Post Hoc
Uji Post Hoc dalam simulasi ini memakai LSD ( uji-t ) dan dapat dilihat penyebab perbedaan berat bangau adalah bangau pada kelompok baris ketiga ( p < 0.05 ).
Dari simulasi ini dapat disimpulkan, bahwa jika ada satu saja individu dalam sebuah kelompok pada populasi yang diuji maka dapat ditarik kesimpulan terdapat perbedaan, walaupun tanpa menguji Anova.
Comments