Uji heteroskedastisitas

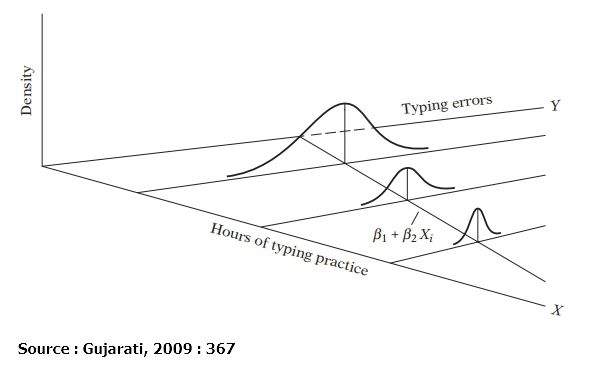
Heteroskedastisitas pada sebuah model menggamparkan pengaruh variabel bebas di luar model. Analisis regresi digunakan untuk melakukan estimasi pada sebuah model untuk n sampel yang berbeda. Tepat tidaknya estimasi regresi sangat tergantung pada dipenuhi tidaknya BLUE (best linier unbias estimated) yang berdasar pada asumsi klasik, di antaranya uji heteroskedastisitas. Jika model melanggar asumsi heteroskedastisitas maka konsekuensinya estimasi menjadi keliru (Gujarati, 2009).

Model umum regresi : Y = b₀ + b_iX_i + μ

Simbol μ merupakan pengganggu model, atau selain X_i. Ini berarti uji heteroskedastisitas adalah pengujian pengaruh selain variabel bebas X_i terhadap variabel Y.

Ada dua kemungkinan estimasi sebagai akibat variabel pengganggu μ, yaitu (Spatz, 2008):

• Jika determinan R² > 70% maka variabel pengganggu tidak terlalu mempengaruhi estimasi (model estimasi bebas dari masalah heteroskedastisitas). Model regresi dapat ditulis tanpa faktor pengganggu, yaitu :
  Y = b₀ + b_iX_i;
• Jika determinan R² < 70% maka variabel pengganggu mempengaruhi estimasi (terjadi masalah heteroskedastisitas). Model regresi justru ditulis tanpa variabel bebas X_i, yaitu :
  Y = b₀ + μ
  

Akibat gejala heteroskedastisitas

Jika model regresi mengalami heteroskedastisitas maka estimasi regresi keliru atau bahkan tidak tepat.

Sebagai ilustrasi produksi sawi (Y) dipengaruhi luas lahan, bibit, pupuk dan pestisida. Gulma atau rumput liar sebagai variabel pengganggu μ karena mungkin saja akibat pemupukan justru akan menyuburkan rumput liar. Akibatnya produksi sawi justru akan berkurang dengan semakin banyaknya pupuk yang diberikan karena gulmapun menjadi tumbuh subur.

Metode pengujian heteroskedastisitas

Banyak metode untuk menguji heteroskedastisitas, salah satunya adalah uji park gletsyer.
Pada aplikasi eViews hanya mengklik View pada output regresi.

Dengan SPSS langkahnya sebagai berikut :

1. Lakukan regresi seperti biasa
2. Pilih option Save
3. Klik menu Transform ▷ Compute Variable untuk membuat variabel absres.
4. Lakukan regresi kembali dengan menjadikan absres sebagai variabel dependent.

Video tutorial

➬

Instagram akun MikroStat video tentang Uji heteroskedastisitas

Kriteria bebas heteroskedastisitas

Probabilitas (p) semua variabel bebas X_i > 5%. Figure 2. Contoh output uji heteroskedastisitas dengan aplikasi eViews. Figure 3. Contoh output uji heteroskedastisitas dengan aplikasi SPSS.

Nilai yang harus diperhatikan pada angka-angka yang dilingkari merah (jika p > 0.05 berarti bebas gejala heteroskedastisitas). Beberapa literatur ada yang memilih dengan kriteria F_test (lingkaran hijau).