Koefisien Determinan

Koefisien determinan ( R² ) merupakan konstanta yang menunjukkan besarnya variasi Y_i setiap terjadi perubahan satu satuan X_i (Gujarati, 2009). Dalam implementasi keseharian, bisa diartikan sebagai besarnya pengaruh variabel X_i terhadap variabel Y yang dinyatakan dalam prosen. Sebagai contoh, berapa persen pengaruh penyiraman terhadap luas daun (lustrasi). Secara matematis dapat dituliskan sebagai berikut (Gujarati, 2009 : 201) :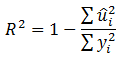


Keterangan :
R²  = Koefisien determinan
u_i  = Nilai residual
y_i  = Nilai observasi

R² Adjusted

Memperhatikan rumus koefisien R² tentu akan menjadi persoalan serius, karena dengan semakin banyaknya variabel bebas X akan menyebabkan nilai R² meningkat walaupun vasiasi perubahan X cenderung konstan. Dalam bahasa statistik, variasi perubahan Y tidak mencerminkan variasi perubahan variabel bebas X sehingga persyaratan BLUE (best linier unbiased estimate) akan dilanggar.
Solusinya adalah untuk model regresi linier berganda (variabel X lebih dari satu) maka harus dilakukan koreksi(dikenal dengan istilah adjusted R²) terhadap rumus baku koefisien R², dengan formulasi sebagai berikut (Gujarati, 2009 : 493)


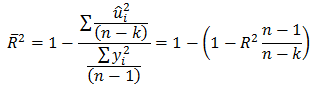
Kesimpulan:
Koefisien determinan R² ➜ regresi linier sederhana.
Adjusted determinan R² ➜ regresi linier berganda.

Untuk ilustrasi dapat dilihat pada contoh berikut:

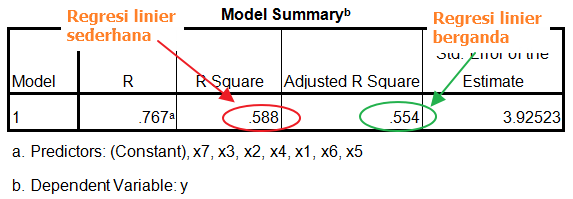
Besaran Determinan

Dalam ilmu sosial, R² > 70% dikatakan tinggi (Gujarati, 2009). Penyebabnya karena Δ (variasi perubahan variabel) X_ij diikuti dengan Δ Y_i. Sebaliknya, jika Δ X_ij tidak diikuti Δ Y_i menyebabkan nilai R² kecil. Gejala yang sering ditemukan karena terdapat data ekstrim (data tidak normal)

Tehnik outlier

Untuk memperbesar nilai R² dengan cara outlier (Gujarati, 2009). Beberapa aplikasi seperti SPSS menyediakan featur outlier (Pallant, 2011) walaupun untuk kasus data panel tidak berjalan efektif (Bisgaard, 2011). Prinsip dasar outlier adalah menghapus data ekstrem (Degroot, 2012), yaitu data di luar μ ± δ

Residual R²

Residu R² merupakan nilai yang menunjukkan pengaruh variabel di luar model. Formulasi residu = 1 - R².
Berdasarkan ilustrasi di atas maka residunya adalah 1 - 0,554 = 0,446 atau sebesar 44,6%.